Recently Bangalore traffic police made a weird move to address traffic problem.
They announced Alternate day commute by own vehicle!
Odd vehicle numbers on odd days and even on even days.
Which means if your vehicle number ends with a odd number, you can take your vehicle out only on odd days!
Many ridiculed this move and bashed them.
I feel an idea is an idea but what made me to post here is the thought...can't we have better ideas than suggesting improve roads, extend roads etc.
Thought I will put some ideas and lets see if it inspires Bangalore traffic police to get more ideas or implement some of these thoughts.
All destinations will have many routes. but one route will always be choked because it might be the shortest.
* encourage car-pooling by ways of charging more when one goes alone or by ways of pushing cars without car-pool to go on a longer route.
* based on Bangalore traffic police idea, I got another idea: Alternate commute on busy routes. Means odd number vehicles one day and even one day. The unlucky day you go by a long route.
This will split the traffic in 2 directions and minimize the burden on one side.
* or split based on type of vehicle. Buses one route, autos one route.
* follow traffic lanes on bigger roads atleast. (auto lane, bus lane etc)
* Do not allow trucks on busy routes in office timings. Ask them to find other ways.
* Avoid big buses and introduce min buses.
* Re-position the bus stops to reduce traffic congestion.
* synchronize the traffic lights to make easier passage.
* Introduce a centralized traffic management systems to monitor and identify busy lines. (I guess they are doing something already, but not sure)
* provide parking complexes and close certain roads as no-motor zone.
* introduce bi-cycles and trolleys in no-motor zone for easy movement of people. (Pick a bi-cycle, commute in the area, park were you leave. make sure bi-cycles and trolleys not to be moved out of the no-motor zone to ensure they are not stolen)
* some of the bangalore buses have GPS and there are websites allow you to track the bus. But very few people utilize this. Reason its not reachable to aam janata. Bring-in more buses with GPS systems. Put electronic boards at stops which will display GPS data of buses in those routes. This helps one to plan their shopping and come on time for the bus.
* introduce cameras at signals and important points which will allow them to monitor traffic and also gives a strong signal to rude drivers that someone is watching and they need to be careful.
* allow flexible working times ex some start working at 8am, some at 9am, some at 10 am etc coordinated by someone.
* if cycling is to be encouraged, needs changing /shower rooms in offices etc. atleast the new corporates can definitely do this.
* provide dedicated bus/cycle lanes, publicize identified cycling routes etc
* discourage single user car usage, starting with the BIG BABUS, INCL MNC Staff
*Enforce all private travels to start from outside city. Let them figure out ways to take passengers outskirts using sumos or other mini buses
* no parking should be strictly enforced on busy roads at peak hours atleast.
* introduce times of commute like no autos between 9-10AM or something similar.
There might be some duplicates so please ignore them.
Lets see if anyone has better ideas.
Sunday, February 03, 2008
Wednesday, January 02, 2008
Happy new year
First of all Wish you all a very happy new year.
I was away from blogging for sometime.
Ok after wishes generally people ask what is your new year resolution.
Let me jot down some of the important things I wish to do this year with respect to blogging.
Firstly I wish to be active blogger.
secondly I plan to start another blog dedicated to Unix.
I was using Unix from the day I know computers. From my college days to work.
Linux was the first one which I started with and Solaris was a dream OS to work on when I was in college. Luckily I got in Sun and working for Solaris team for the past 4 years.
Being part of Solaris team and having fair understanding about the unix world, I thought I will start a blog on Unix with focus on Solaris.
http://unixlessons.blogspot.com/
Lets see how it goes.
I was away from blogging for sometime.
Ok after wishes generally people ask what is your new year resolution.
Let me jot down some of the important things I wish to do this year with respect to blogging.
Firstly I wish to be active blogger.
secondly I plan to start another blog dedicated to Unix.
I was using Unix from the day I know computers. From my college days to work.
Linux was the first one which I started with and Solaris was a dream OS to work on when I was in college. Luckily I got in Sun and working for Solaris team for the past 4 years.
Being part of Solaris team and having fair understanding about the unix world, I thought I will start a blog on Unix with focus on Solaris.
http://unixlessons.blogspot.com/
Lets see how it goes.
Thursday, November 16, 2006
Vedic Mathematics
Vedas are the knowledge houses and the pillars of our dharma and culture. Each sloka embeds meaning in a multi dimensional way. Many Rushis did research on these Vedic content and each one interpreted Vedas in their own way. (The very reason for so many Upanishads)
Unfortunately the research done by the Rushis (mostly on the spiritual fronts) is not transfered properly to the generations later.
Research was limited to the Sishya brunda and/or passed to the next generation from father to son. Which dis-integrated over a period of time.
Also our ancestors never bothered about proving something that was derived (Probably they considered its too obvious which we are not able to interpret now) and saving the content other than transferring from one mind to other.
Vedic Mathematics comes from Atharvana Veda which deals with Science. Vedic mathematics was explored by His Holiness Jagadguru Sankaracharya Sri Bharati Krsna Tirthaji Maharaja of Puri math. (Govardhana Matha). He explored the cryptic Vedic mysteries from Atharvana Veda.
In Sri Shankaracharya's words:
"The very word 'Veda' has a derivational meaning, i.e. the fountainhead and illimitable store-house of all knowledge. This derivation, in effect, means, connotes and implies that the Vedas should contain within themselves all the knowledge needed by mankind relating not only to the so-called 'Spiritual' matters but also to those usually described as purely 'secular', 'temporal' or 'wordly' and also to the means required by humanity as such for the achievement of all-round, complete and perfect success in all conceivable directions and that there can be no adjectival or restrictive epithet calculated to limit that knowledge down in any sphere, any direction or any respect whatsoever.
In other words, it connotes and implies that our ancient Indian Vedic lore should be all-around, complete and perfect and able to throw the fullest necessary light on all matters which any aspiring seeker after knowledge can possibly seek to be enlightened on"
There are 4 Vedas, 4 Upavedas and 6 Vedangas.
Swamiji Discovered 16 Sutras, based on which the Whole Vedic Mathematics is derived, comes under Parisistas for Atharvana Veda.
Swamiji, at an age of 20, completed MA in 7 subjects (Sanskrit, Philosophy, English, Mathematics, History and Science) which was a record at that time.
He worked as a principal before he moved to Sringeri for doing research in Vedas.
He spent 8 years reading the manu-scripts while doing thapa in the near-by forest at Sringeri, during which he wrote 16 volumes based on all these 16 sutras covering many areas of Mathematics existing now and Mathematics which is not yet known to this world.
Unfortunately these 16 volumes which he wrote were deposited in a near-by disciples house, which were lost when Swamiji wanted to collect it back after few years.
Still Swamiji mentioned that its all in his mind and can re-write the work again.
He started his work with an Introductory volume (which is the only source for Vedic Mathematics now), followed by 16 volumes which he apparently couldn't complete because his health deteriorated so badly and couldn't complete before he attained Mukthi.
I will not discuss about the 16 Sutras he derived as many are available on internet.
But would like to emphasize on the manifold and multifarious meanings of slokas in our Vedic literature. The first step in his success is to understood the Vedic Numerical code in Vedas.
Ancients, when big numbers are needed to represent, they didn't use symbols rather used the letters of Sanskrit to represent. And few numbers are so important that they needed to get it by heart.
So Sanskrit verses were written to easily by heart and remember such numbers.
heres the key which he gave:
कादि नव, टादि नव, पादि पसचक, याद्यष्तक क्ष: सून्याम
ka and the following 8 letters; ta and the following 8 letters; pa and the following 4 letters;
ya and the following seven letters; and ksa for zero.
to elaborate a bit more
The code used is as follows:
The Sanskrit consonants
ka, ta, pa, and ya all denote 1;
kha, tha, pha, and ra all represent 2;
ga, da, ba, and la all stand for 3;
Gha, dha, bha, and va all represent 4;
gna, na, ma, and sa all represent 5;
ca, ta, and sa all stand for 6;
cha, tha, and sa all denote 7;
ja, da, and ha all represent 8;
jha and dha stand for 9; and
ka means zero.
Vowels make no difference and it is left to the author to select a particular consonant or vowel at each step. This great latitude allows one to bring about additional meanings of his own choice. For example kapa, tapa, papa, and yapa all mean 11.
By a particular choice of consonants and vowels one can compose a poetic hymn with double or triple meanings. Here is an actual sutra of spiritual content, as well as secular mathematical significance:
गोपी भा ग्या माधुवरत-श्रृगी शोदधीसंधिग
खाला जीवितखाटाव गलाहालारसंधर
(I used quillpad to convert. Not able to get appropriately. so again giving in English)
gopi bhagya madhuvrata
srngiso dadhi sandhiga
khala jivita khatava
gala hala rasandara
While this verse is a petition to Lord Krishna, when learning it one can also learn the value of pi/10 (i.e. the ratio of the circumference of a circle to its diameter divided by 10) to 32 decimal places. It has a self-contained master-key for extending the review to any number of decimal places. The translation is as follows: "O Lord anointed with the yoghurt of the milkmaids' worship (Krishna), O saviour of the fallen, O master of Shiva, please protect me."
At the same time, by application of the consonant code given above, this verse directly yields the decimal equivalent of pi divided by 10: pi/10 = 0.31415926535897932384626433832792. Thus, while offering mantric praise to Godhead in devotion, by this method one can also add to memory significant secular truths.
Some Universities which are working on Vedic Mathematics
(I searched in google to find this. Maybe there are more Universities working on this which I don't know)
http://www.floridavediccollege.edu (chk out the people working in this clge. none are Indians)
http://www.mum.edu
http://www.cuhcs.org.uk
http://www.matrixedu.org
http://www.clarku.edu
some of the papers/research work based on Vedic Mathematics.
(Only the papers which I was able to find are listed here)
* The Implementation of Vedic Algorithms in Digital Signal Processing*
* Design and analysis of a novel parallel square and cube architecture based on ancient Indian Vedic mathematics
* VLSI implementation of RSA encryption system using ancient Indian Vedic mathematics
* Vedic multiplier with fast carry optimization
* Presenting Proofs Using Logicographic Symbols
* An efficient method of elliptic curve encryption using Ancient Indian Vedic Mathematics
books:
I don't want to copy paste here. Search Vedic Mathematics in amazon.com and see how many books are available.
I would suggest you to buy the Vedic Mathematics book by Jagadguru Swami Sri Bharati Krsna Tirthaji Maharaja from Motilal Banarsidas publications. (A 125/- book, I guess, which the source for many books available in bookstores)
Unfortunately the research done by the Rushis (mostly on the spiritual fronts) is not transfered properly to the generations later.
Research was limited to the Sishya brunda and/or passed to the next generation from father to son. Which dis-integrated over a period of time.
Also our ancestors never bothered about proving something that was derived (Probably they considered its too obvious which we are not able to interpret now) and saving the content other than transferring from one mind to other.
Vedic Mathematics comes from Atharvana Veda which deals with Science. Vedic mathematics was explored by His Holiness Jagadguru Sankaracharya Sri Bharati Krsna Tirthaji Maharaja of Puri math. (Govardhana Matha). He explored the cryptic Vedic mysteries from Atharvana Veda.
In Sri Shankaracharya's words:
"The very word 'Veda' has a derivational meaning, i.e. the fountainhead and illimitable store-house of all knowledge. This derivation, in effect, means, connotes and implies that the Vedas should contain within themselves all the knowledge needed by mankind relating not only to the so-called 'Spiritual' matters but also to those usually described as purely 'secular', 'temporal' or 'wordly' and also to the means required by humanity as such for the achievement of all-round, complete and perfect success in all conceivable directions and that there can be no adjectival or restrictive epithet calculated to limit that knowledge down in any sphere, any direction or any respect whatsoever.
In other words, it connotes and implies that our ancient Indian Vedic lore should be all-around, complete and perfect and able to throw the fullest necessary light on all matters which any aspiring seeker after knowledge can possibly seek to be enlightened on"
There are 4 Vedas, 4 Upavedas and 6 Vedangas.
Swamiji Discovered 16 Sutras, based on which the Whole Vedic Mathematics is derived, comes under Parisistas for Atharvana Veda.
Swamiji, at an age of 20, completed MA in 7 subjects (Sanskrit, Philosophy, English, Mathematics, History and Science) which was a record at that time.
He worked as a principal before he moved to Sringeri for doing research in Vedas.
He spent 8 years reading the manu-scripts while doing thapa in the near-by forest at Sringeri, during which he wrote 16 volumes based on all these 16 sutras covering many areas of Mathematics existing now and Mathematics which is not yet known to this world.
Unfortunately these 16 volumes which he wrote were deposited in a near-by disciples house, which were lost when Swamiji wanted to collect it back after few years.
Still Swamiji mentioned that its all in his mind and can re-write the work again.
He started his work with an Introductory volume (which is the only source for Vedic Mathematics now), followed by 16 volumes which he apparently couldn't complete because his health deteriorated so badly and couldn't complete before he attained Mukthi.
I will not discuss about the 16 Sutras he derived as many are available on internet.
But would like to emphasize on the manifold and multifarious meanings of slokas in our Vedic literature. The first step in his success is to understood the Vedic Numerical code in Vedas.
Ancients, when big numbers are needed to represent, they didn't use symbols rather used the letters of Sanskrit to represent. And few numbers are so important that they needed to get it by heart.
So Sanskrit verses were written to easily by heart and remember such numbers.
heres the key which he gave:
कादि नव, टादि नव, पादि पसचक, याद्यष्तक क्ष: सून्याम
ka and the following 8 letters; ta and the following 8 letters; pa and the following 4 letters;
ya and the following seven letters; and ksa for zero.
to elaborate a bit more
The code used is as follows:
The Sanskrit consonants
ka, ta, pa, and ya all denote 1;
kha, tha, pha, and ra all represent 2;
ga, da, ba, and la all stand for 3;
Gha, dha, bha, and va all represent 4;
gna, na, ma, and sa all represent 5;
ca, ta, and sa all stand for 6;
cha, tha, and sa all denote 7;
ja, da, and ha all represent 8;
jha and dha stand for 9; and
ka means zero.
Vowels make no difference and it is left to the author to select a particular consonant or vowel at each step. This great latitude allows one to bring about additional meanings of his own choice. For example kapa, tapa, papa, and yapa all mean 11.
By a particular choice of consonants and vowels one can compose a poetic hymn with double or triple meanings. Here is an actual sutra of spiritual content, as well as secular mathematical significance:
गोपी भा ग्या माधुवरत-श्रृगी शोदधीसंधिग
खाला जीवितखाटाव गलाहालारसंधर
(I used quillpad to convert. Not able to get appropriately. so again giving in English)
gopi bhagya madhuvrata
srngiso dadhi sandhiga
khala jivita khatava
gala hala rasandara
While this verse is a petition to Lord Krishna, when learning it one can also learn the value of pi/10 (i.e. the ratio of the circumference of a circle to its diameter divided by 10) to 32 decimal places. It has a self-contained master-key for extending the review to any number of decimal places. The translation is as follows: "O Lord anointed with the yoghurt of the milkmaids' worship (Krishna), O saviour of the fallen, O master of Shiva, please protect me."
At the same time, by application of the consonant code given above, this verse directly yields the decimal equivalent of pi divided by 10: pi/10 = 0.31415926535897932384626433832792. Thus, while offering mantric praise to Godhead in devotion, by this method one can also add to memory significant secular truths.
Some Universities which are working on Vedic Mathematics
(I searched in google to find this. Maybe there are more Universities working on this which I don't know)
http://www.floridavediccollege.edu (chk out the people working in this clge. none are Indians)
http://www.mum.edu
http://www.cuhcs.org.uk
http://www.matrixedu.org
http://www.clarku.edu
some of the papers/research work based on Vedic Mathematics.
(Only the papers which I was able to find are listed here)
* The Implementation of Vedic Algorithms in Digital Signal Processing*
* Design and analysis of a novel parallel square and cube architecture based on ancient Indian Vedic mathematics
* VLSI implementation of RSA encryption system using ancient Indian Vedic mathematics
* Vedic multiplier with fast carry optimization
* Presenting Proofs Using Logicographic Symbols
* An efficient method of elliptic curve encryption using Ancient Indian Vedic Mathematics
books:
I don't want to copy paste here. Search Vedic Mathematics in amazon.com and see how many books are available.
I would suggest you to buy the Vedic Mathematics book by Jagadguru Swami Sri Bharati Krsna Tirthaji Maharaja from Motilal Banarsidas publications. (A 125/- book, I guess, which the source for many books available in bookstores)
Sunday, October 01, 2006
Govinduni Brahmotsavam
"GOvindaaSrita gOkula brundaa paavana jayajaya paramaananda"
Govinda namam paramaanandam, Brahmotsavam brahmaanandam.
The Brahmotsavam is an annual festival celebrated on Tirumala for nine days when the sun enters Kanya Rashi from Ashwayuja Shuddha Padyami to Ashwayuja Shuddha Dashami during September/October time period. This year its between 25th September and 3rd October.
Its a nine day fest starting with
Day 1:
style="font-weight:bold;">Dhwajarohana, is conducted by hoisting the Garudadhwaja (flag with the emblem of a black garuda), near the Srivari Alaya Dhwajasthambham. Then lords procession on Pedda Seshavahana (vehicle shaped like Adisesha) in the maada veedhis. (maada veedhi: 4 roads surrounding the temple, where the procession happens)
day2:
Chinna Seshavahana in the morning.
Night Unjal Seva and procession on Hamsavahana.
Unjal seva is conducted almost everyday of the brahmotsavam except on day 6.
day3:
Simhavahana
Mutayalapandiri Vahana
day4:
Kalpavriksha Vahana
Sarvabhoopala Vahana.
day5:
Mohini Avatarotsavam
Garuda Vahana.
Garuda vahana has utmost importance and a large number of pilgrims visit on that day. I heard this time the maada veedhi is full of pilgrims.
Garuda is also called periyatiruvadi, meaning the first devotee.
day6:
hanumad Vahana.
Unjal Seva is not performed today. Instead, Vasantotsavam (spring festival) is celebrated.
In the night, the Lord is mounted on the Gaja Vahana.
day7:
Suryaprabha Vahana
Chandraprabha Vahana
day8:
Rathotsavam is celebrated, in which the Lord is seated in a ratham (chariot) and taken in a procession in the morning.
Rathostham kesavam dristva punarjanma na vidyate, means whoever witness Rathotsavam will not be reborn.
The idols of Daruka (the charioteer of Lord Sri Krishna) and the four horses (Saibyam, Sugreevam, Meghapushpam and Valahakam) are placed before the decorated deities of the Lord and his consorts. This symbolises that the lord’s charioteer is driving the chariot.
The chariot is pulled along by devotees, who chant Govinda!, Govinda! This is the only opportunity that devotees get to be of service to the Lord during Brahmotsavam.

After the Unjal Seva in the night, the deities are taken in the Aswa (horse) Vahana.
day9:
Pallaki Seva and Chakrasnana Mahotsavam in the morning and Dhwajavarohanam are performed in the evening.
My parents, staying in Tirupati, were desperately trying to go there to participate in this event. Man proposes, god disposes. But finally we got a call from lord to participate. We planned to go on Sunday morning for the Surya Prabha vahana, but puja in our house was not over by then, so we planned in the evening. Mom and dad finished their evening rituals and we started around 6:30PM. Our driver, Ramana, who knows in-and-outs of all roads in Tirumala, parked the car close to one of the maada veedhis.
There's a narrow lane through the bushes which leads to the maada veedhi. Its hardly 50 yards. We were there well before the scheduled time of start(9:30PM)

I went around taking pics. The decoration was simply superb, everyone in their traditional attires...dancing, singing, praying; elephants, horses, cows all decorated well; trees, plants all covered with lights. I saw in the TV but I should say its different over there.

Finally lord appeared on Chandraprabha Vahana (moon-shaped vehicle)
According to Hindu mythology, Chandra is the commander of the mind and the king of aushadha (medicine). It is also said that riding on the Chandraprabha Vahana is a soothing experience for the Lord that brings peace to devotees' minds.

It started raining, but very little. My mom offered dry fruits to lord. As the procession left that place, within few minutes she was surronded by pilgrims for the prasad, we distributed and quickly ran to our car as the dripping rain started heavily. We crawled down the hill slowly due to the heavy downpour. We reached home around 11:30PM. Overall a wonderful experience and a must visit for everyone atleast once in their lifetime for brahmotsavam.
Please visit the following links for more info:
http://www.tirumala.org/utsavams_brahmo_activities.htm
http://www.srivaishnava.org/customs/butsav_T.html
http://www.templenet.com/bhram.html
Om namo venkatesaya
Govinda namam paramaanandam, Brahmotsavam brahmaanandam.
The Brahmotsavam is an annual festival celebrated on Tirumala for nine days when the sun enters Kanya Rashi from Ashwayuja Shuddha Padyami to Ashwayuja Shuddha Dashami during September/October time period. This year its between 25th September and 3rd October.
Its a nine day fest starting with
Day 1:
style="font-weight:bold;">Dhwajarohana, is conducted by hoisting the Garudadhwaja (flag with the emblem of a black garuda), near the Srivari Alaya Dhwajasthambham. Then lords procession on Pedda Seshavahana (vehicle shaped like Adisesha) in the maada veedhis. (maada veedhi: 4 roads surrounding the temple, where the procession happens)
day2:
Chinna Seshavahana in the morning.
Night Unjal Seva and procession on Hamsavahana.
Unjal seva is conducted almost everyday of the brahmotsavam except on day 6.
day3:
Simhavahana
Mutayalapandiri Vahana
day4:
Kalpavriksha Vahana
Sarvabhoopala Vahana.
day5:
Mohini Avatarotsavam
Garuda Vahana.
Garuda vahana has utmost importance and a large number of pilgrims visit on that day. I heard this time the maada veedhi is full of pilgrims.
Garuda is also called periyatiruvadi, meaning the first devotee.
day6:
hanumad Vahana.
Unjal Seva is not performed today. Instead, Vasantotsavam (spring festival) is celebrated.
In the night, the Lord is mounted on the Gaja Vahana.
day7:
Suryaprabha Vahana
Chandraprabha Vahana
day8:
Rathotsavam is celebrated, in which the Lord is seated in a ratham (chariot) and taken in a procession in the morning.
Rathostham kesavam dristva punarjanma na vidyate, means whoever witness Rathotsavam will not be reborn.
The idols of Daruka (the charioteer of Lord Sri Krishna) and the four horses (Saibyam, Sugreevam, Meghapushpam and Valahakam) are placed before the decorated deities of the Lord and his consorts. This symbolises that the lord’s charioteer is driving the chariot.
The chariot is pulled along by devotees, who chant Govinda!, Govinda! This is the only opportunity that devotees get to be of service to the Lord during Brahmotsavam.

After the Unjal Seva in the night, the deities are taken in the Aswa (horse) Vahana.
day9:
Pallaki Seva and Chakrasnana Mahotsavam in the morning and Dhwajavarohanam are performed in the evening.
My parents, staying in Tirupati, were desperately trying to go there to participate in this event. Man proposes, god disposes. But finally we got a call from lord to participate. We planned to go on Sunday morning for the Surya Prabha vahana, but puja in our house was not over by then, so we planned in the evening. Mom and dad finished their evening rituals and we started around 6:30PM. Our driver, Ramana, who knows in-and-outs of all roads in Tirumala, parked the car close to one of the maada veedhis.
There's a narrow lane through the bushes which leads to the maada veedhi. Its hardly 50 yards. We were there well before the scheduled time of start(9:30PM)

I went around taking pics. The decoration was simply superb, everyone in their traditional attires...dancing, singing, praying; elephants, horses, cows all decorated well; trees, plants all covered with lights. I saw in the TV but I should say its different over there.

Finally lord appeared on Chandraprabha Vahana (moon-shaped vehicle)
According to Hindu mythology, Chandra is the commander of the mind and the king of aushadha (medicine). It is also said that riding on the Chandraprabha Vahana is a soothing experience for the Lord that brings peace to devotees' minds.

It started raining, but very little. My mom offered dry fruits to lord. As the procession left that place, within few minutes she was surronded by pilgrims for the prasad, we distributed and quickly ran to our car as the dripping rain started heavily. We crawled down the hill slowly due to the heavy downpour. We reached home around 11:30PM. Overall a wonderful experience and a must visit for everyone atleast once in their lifetime for brahmotsavam.
Please visit the following links for more info:
http://www.tirumala.org/utsavams_brahmo_activities.htm
http://www.srivaishnava.org/customs/butsav_T.html
http://www.templenet.com/bhram.html
Om namo venkatesaya
Sunday, September 24, 2006
My new friend, Ramesh
hmm I thought my blog will motivate few people at least...so the reason why I am blogging this.
I go to office on auto-rickshaw daily. It costs me around 25/- one side.
I live is ulsoor a crowded area in Bangalore and I live close to the center.
Also the bus stop is around 100 yards.
Fortunately my company is near Richmond circle which is close to the bus stop.
But on return, the bus stop is too far as its one way...I have to go to residency road to catch a bus.
I just don't go by bus in the morning because its crowded always and I will be tired when I reach office. So I don't go by bus.
But recently I observed a crippled person, called Ramesh, comes daily to the bus stop and is begging. I generally don't encourage beggars, but this person needs support and encouragement.

I decided I have to quit auto-rickshaw on one side and give some money to this guy.
I go to this guy daily, give around 10/- and ask him how he is,
what he did yesterday etc stuff till I get my bus. He knows only kannada,
but I manage to communicate with him.
He is a shy person, but now I developed a rapo with Ramesh...now he recognizes me from a distance and gives me a warn welcome. He gives me a beautiful smile and makes my day.
Who benefited from this? ofcourse its me. I save around 5 to 10/- per day and also gets affection from this sweet new friend.
I took his picture and promised him will give one day.
Look at him in this pic...do you think I got this smile because of money I give?...absolutely not.

You need to care someone to gain affection. Yes I am selfish...but there is happiness to be selfish like this.
I go to office on auto-rickshaw daily. It costs me around 25/- one side.
I live is ulsoor a crowded area in Bangalore and I live close to the center.
Also the bus stop is around 100 yards.
Fortunately my company is near Richmond circle which is close to the bus stop.
But on return, the bus stop is too far as its one way...I have to go to residency road to catch a bus.
I just don't go by bus in the morning because its crowded always and I will be tired when I reach office. So I don't go by bus.
But recently I observed a crippled person, called Ramesh, comes daily to the bus stop and is begging. I generally don't encourage beggars, but this person needs support and encouragement.

I decided I have to quit auto-rickshaw on one side and give some money to this guy.
I go to this guy daily, give around 10/- and ask him how he is,
what he did yesterday etc stuff till I get my bus. He knows only kannada,
but I manage to communicate with him.
He is a shy person, but now I developed a rapo with Ramesh...now he recognizes me from a distance and gives me a warn welcome. He gives me a beautiful smile and makes my day.
Who benefited from this? ofcourse its me. I save around 5 to 10/- per day and also gets affection from this sweet new friend.
I took his picture and promised him will give one day.
Look at him in this pic...do you think I got this smile because of money I give?...absolutely not.

You need to care someone to gain affection. Yes I am selfish...but there is happiness to be selfish like this.
Sunday, August 06, 2006
The Story of Fibonacci Series.
I am currently on vacation and my eye caught this master piece in the shelf, The Art of computer programming by Donald Knuth. I always wanted to complete all the volumes which are available in the market.
Rightnow I have the first 3 voulmes of this book. I tried to read these books, to completion, but never was able to. :-(
I did Randomized Algorithms course in IIT, so I read Volume II to some extent.
Randomized Algorithms course was interesting as each time our prof gave a new algorithm, he used to say "Now that we know this algo, so its no more random, as we can predict the next number using this algorithm :-)"
Finally He concluded the course saying theres no truly Random Algorithm existing in this world. So whats the point in doing this course :-O
I was just skimming through Volume I of this book (Knuth) and saw the section about the famous series, Fibonacci Series.
This reminded me of a the program I did long back, when I was in college, which prints all the fibonacci numbers. Fibonacci numbers are mentioned in Dan Brown's novel DaVinci Code. Many of you might know about Fibonacci numbers through this book, but a computer science grad will definitely kow about Fibonacci series...even the mathematics grad should be knowing about these sequesnce. But many of then don't know the importance of this series.
The algorithm is simple:
If F(n) is the nth fibonacci number then
F(n) is 1 for n = 1, 2
F(n) = F(n-1) + F(n-2) where n>2
At that time, I was curious why we are doing this program. All I could know is this is one example for writing a recursive program.
I wrote GCD:
GCD(m,n) = GCD(n,m), if n>m;
= m if n=0;
= GCD(n, m%n), otherwise.
I wrote Ackermann's function:
A(0,n) = n+1;
A(m+1,0) = A(m,1);
A(m+1,n+1) = A(m, A(m+1,n))
But I felt both these functions are of importance. GCD...we know about it, Ackermanns function is one of the fastest growing primitive recursive function I know till date. (consider f(x) = A(x,x) then for x = 0,1,2,3,4, g(x) values are 1,3,7,61, 2^2^2^65,536 -3 :-O ( where ^ is to-the-power-of)
Well, I tend to divert from the actual topic:-D, let me get back. I know GCD or ackermann's functions has some importance, but why Fibonacci numbers? :-O
No idea then, but this curiosity made me investigate what this fibonacci numbers are....
Fibonacci numbers were invented by Leonardo Pisano in 1100AD. Before Fibonacci (Leonardo's another name) wrote his work, the sequence Fn had already been discussed by Indian scholars, who had long been interested in rhythmic patterns that are formed from one-beat and two-beat notes. The number of such rhythms having n beats altogether is Fn+1; therefore both Gospala (before 1135) and Hemachandra (c. 1150) mentioned the numbers 1, 2, 3, 5, 8, 13, 21, ... explicitly. (Snip taken from a website. forgot the link :-( )
Fibonacci mentioned a problem in his books...
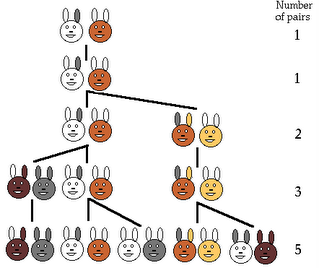
How Many Pairs of Rabbits Are Created by One Pair in One Year?
A certain man had one pair of rabbits together in a certain enclosed place, and one wishes to know how many are created from the pair in one year when it is the nature of them in a single month to bear another pair, and in the second month those born to bear also.
He then goes on to solve and explain the solution:
Because the abovewritten pair in the first month bore, you will double it; there will be two pairs in one month. One of these, namely the first, bears in the second month, and thus there are in the second month 3 pairs; of these in one month two are pregnant and in the third month 2 pairs of rabbits are born, and thus there are 5 pairs in the month;
...
there will be 144 pairs in this [the tenth] month; to these are added again the 89 pairs that are born in the eleventh month; there will be 233 pairs in this month. To these are still added the 144 pairs that are born in the last month; there will be 377 pairs, and this many pairs are produced from the abovewritten pair in the mentioned place at the end of the one year.
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the abovewritten sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.
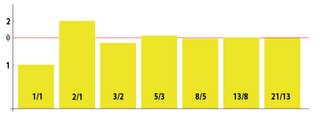
The ratios of successive Fibonacci numbers F(n)/F(n-1) approaches the golden ratio phi as n approaches infinity.
What is Golden Ratio..hey wait, this would be fun to know, but wait for next post. :-)
Some interesting properties of Fibonacci numbers.
We see Fibonacci numbers in biology:
Phyllotaxis: (The following snip was taken from mathworld.wolfram.com)
The beautiful arrangement of leaves in some plants, called phyllotaxis, obeys a number of subtle mathematical relationships. For instance, the florets in the head of a sunflower form two oppositely directed spirals: 55 of them clockwise and 34 counterclockwise. Surprisingly, these numbers are consecutive Fibonacci numbers. The ratios of alternate Fibonacci numbers are given by the convergents to phi^(-2), where phi is the golden ratio, and are said to measure the fraction of a turn between successive leaves on the stalk of a plant: 1/2 for elm and linden, 1/3 for beech and hazel, 2/5 for oak and apple, 3/8 for poplar and rose, 5/13 for willow and almond, etc. (Coxeter 1969, Ball and Coxeter 1987). A similar phenomenon occurs for daisies, pineapples, pinecones, cauliflowers, and so on.
Lilies, irises, and the trillium have three petals; columbines, buttercups, larkspur, and wild rose have five petals; delphiniums, bloodroot, and cosmos have eight petals; corn marigolds have 13 petals; asters have 21 petals; and daisies have 34, 55, or 89 petals--all Fibonacci numbers.
 This figure shows the buds 13 in clockwise and 21 in anti-clockwise...both Fibonacci numbers.
This figure shows the buds 13 in clockwise and 21 in anti-clockwise...both Fibonacci numbers.
Some mathematical properties:
1) F(n+1)*F(n-1) - 2*F(n) = (-1) TTPO n
2) GCD(F(m),F(n)) = F(GCD(m,n))
3) F(n) <= phi to-the-power-of (n-1)
4) phi to-the-power-of 2 = phi + 1;
5) phi = (1+sqrt5)/2
6) Fib(n) = round( Phi TTPO n/√5 )
7) Fibonacci numbers are complete, which means you can generate any positive number with the sum of any set of Fibonacci numbers.
8) Neighbouring Fibonacci Numbers have no common factors
9) Any prime Fibonacci number must have a subscript which is prime with one exception. (Go and find it out yourself. ;-) )
10) Can you find out Fibonacci numbers from Pascal's traingle?

There are lot more of such properties in The Art of Computer Programming by D. Knuth.
One of the interesting problem I found in the excercises of this book is
Problem) 2 players complete is a game: There a pile of n chips; 1st player takes as many chips as he like, except he can't take the whole pile.
From then on, players alternate moves, each person can take atmost twice as many chips as the preceeding player has taken. The player who takes the last chip wins.
Now solve this problem ;-)....do you see the usage of Fibonacci numbers here?
Some more properties. Basically you see such questions in interviews ;-)
1) The number of ways of picking a set (including the empty set) from the numbers 1, 2, ..., n without picking two consecutive numbers is F_(n+2). The number of ways of picking a set (including the empty set) from the numbers 1, 2, ..., n without picking two consecutive numbers (where 1 and n are now consecutive) is L_n==F_(n+1)+F_(n-1), where L_n is a Lucas number.
2) The probability of not getting two heads in a row in n tosses of a coin is F_(n+2)/2^n (Honsberger 1985, pp. 120-122). Fibonacci numbers are also related to the number of ways in which n coin tosses can be made such that there are not three consecutive heads or tails. The number of ideals of an n-element fence poset is the Fibonacci number F_n.
3) Given a resistor network of n 1-Omega resistors, each incrementally connected in series or parallel to the preceding resistors, then the net resistance is a rational number having maximum possible denominator of F_(n+1).
Do you know about Fibonacci number system? No I won't mention it here. Go find it yourself :-P
(Hint: search for Fibonaccimal)
Do you realize. KM to Mile conversion we can use Fibonacci numbers?
Yes. 8 Kms is 5 miles, 5 kms is 3 miles....So F(n) Kms is F(n-1) miles!!
What if you have to find 20 Kms in miles. Yep there a solution. convert to Fibonacci number system.
20 can be expressed as 13+5+2. So the miles conversion is 8+3+1=12Miles!!
Note: These are just approximations in Miles, not close values.
Now don't ask me what the value of 1Km in Miles ;-) ...larger values get closer but not accurate approximation.
visit this link for more info
Fibonacci numbers:
http://mathworld.wolfram.com/FibonacciNumber.html
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibrep.html
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/Fibonomials.html
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html
Phyllotaxis:
http://mathworld.wolfram.com/Phyllotaxis.html
http://maven.smith.edu/~phyllo/index.html
Fibonacci numbers in nature:
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
Fibonaccimal Base:
http://acm.up.pt/local/prova2/c.html
Books:
The Art of computer programming, Volume I, by D. Knuth.
Rightnow I have the first 3 voulmes of this book. I tried to read these books, to completion, but never was able to. :-(
I did Randomized Algorithms course in IIT, so I read Volume II to some extent.
Randomized Algorithms course was interesting as each time our prof gave a new algorithm, he used to say "Now that we know this algo, so its no more random, as we can predict the next number using this algorithm :-)"
Finally He concluded the course saying theres no truly Random Algorithm existing in this world. So whats the point in doing this course :-O
I was just skimming through Volume I of this book (Knuth) and saw the section about the famous series, Fibonacci Series.
This reminded me of a the program I did long back, when I was in college, which prints all the fibonacci numbers. Fibonacci numbers are mentioned in Dan Brown's novel DaVinci Code. Many of you might know about Fibonacci numbers through this book, but a computer science grad will definitely kow about Fibonacci series...even the mathematics grad should be knowing about these sequesnce. But many of then don't know the importance of this series.
The algorithm is simple:
If F(n) is the nth fibonacci number then
F(n) is 1 for n = 1, 2
F(n) = F(n-1) + F(n-2) where n>2
At that time, I was curious why we are doing this program. All I could know is this is one example for writing a recursive program.
I wrote GCD:
GCD(m,n) = GCD(n,m), if n>m;
= m if n=0;
= GCD(n, m%n), otherwise.
I wrote Ackermann's function:
A(0,n) = n+1;
A(m+1,0) = A(m,1);
A(m+1,n+1) = A(m, A(m+1,n))
But I felt both these functions are of importance. GCD...we know about it, Ackermanns function is one of the fastest growing primitive recursive function I know till date. (consider f(x) = A(x,x) then for x = 0,1,2,3,4, g(x) values are 1,3,7,61, 2^2^2^65,536 -3 :-O ( where ^ is to-the-power-of)
Well, I tend to divert from the actual topic:-D, let me get back. I know GCD or ackermann's functions has some importance, but why Fibonacci numbers? :-O
No idea then, but this curiosity made me investigate what this fibonacci numbers are....
Fibonacci numbers were invented by Leonardo Pisano in 1100AD. Before Fibonacci (Leonardo's another name) wrote his work, the sequence Fn had already been discussed by Indian scholars, who had long been interested in rhythmic patterns that are formed from one-beat and two-beat notes. The number of such rhythms having n beats altogether is Fn+1; therefore both Gospala (before 1135) and Hemachandra (c. 1150) mentioned the numbers 1, 2, 3, 5, 8, 13, 21, ... explicitly. (Snip taken from a website. forgot the link :-( )
Fibonacci mentioned a problem in his books...
How Many Pairs of Rabbits Are Created by One Pair in One Year?
A certain man had one pair of rabbits together in a certain enclosed place, and one wishes to know how many are created from the pair in one year when it is the nature of them in a single month to bear another pair, and in the second month those born to bear also.
He then goes on to solve and explain the solution:
Because the abovewritten pair in the first month bore, you will double it; there will be two pairs in one month. One of these, namely the first, bears in the second month, and thus there are in the second month 3 pairs; of these in one month two are pregnant and in the third month 2 pairs of rabbits are born, and thus there are 5 pairs in the month;
...
there will be 144 pairs in this [the tenth] month; to these are added again the 89 pairs that are born in the eleventh month; there will be 233 pairs in this month. To these are still added the 144 pairs that are born in the last month; there will be 377 pairs, and this many pairs are produced from the abovewritten pair in the mentioned place at the end of the one year.
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the abovewritten sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.

The ratios of successive Fibonacci numbers F(n)/F(n-1) approaches the golden ratio phi as n approaches infinity.

What is Golden Ratio..hey wait, this would be fun to know, but wait for next post. :-)
Some interesting properties of Fibonacci numbers.
We see Fibonacci numbers in biology:
Phyllotaxis: (The following snip was taken from mathworld.wolfram.com)
The beautiful arrangement of leaves in some plants, called phyllotaxis, obeys a number of subtle mathematical relationships. For instance, the florets in the head of a sunflower form two oppositely directed spirals: 55 of them clockwise and 34 counterclockwise. Surprisingly, these numbers are consecutive Fibonacci numbers. The ratios of alternate Fibonacci numbers are given by the convergents to phi^(-2), where phi is the golden ratio, and are said to measure the fraction of a turn between successive leaves on the stalk of a plant: 1/2 for elm and linden, 1/3 for beech and hazel, 2/5 for oak and apple, 3/8 for poplar and rose, 5/13 for willow and almond, etc. (Coxeter 1969, Ball and Coxeter 1987). A similar phenomenon occurs for daisies, pineapples, pinecones, cauliflowers, and so on.
Lilies, irises, and the trillium have three petals; columbines, buttercups, larkspur, and wild rose have five petals; delphiniums, bloodroot, and cosmos have eight petals; corn marigolds have 13 petals; asters have 21 petals; and daisies have 34, 55, or 89 petals--all Fibonacci numbers.
 This figure shows the buds 13 in clockwise and 21 in anti-clockwise...both Fibonacci numbers.
This figure shows the buds 13 in clockwise and 21 in anti-clockwise...both Fibonacci numbers.Some mathematical properties:
1) F(n+1)*F(n-1) - 2*F(n) = (-1) TTPO n
2) GCD(F(m),F(n)) = F(GCD(m,n))
3) F(n) <= phi to-the-power-of (n-1)
4) phi to-the-power-of 2 = phi + 1;
5) phi = (1+sqrt5)/2
6) Fib(n) = round( Phi TTPO n/√5 )
7) Fibonacci numbers are complete, which means you can generate any positive number with the sum of any set of Fibonacci numbers.
8) Neighbouring Fibonacci Numbers have no common factors
9) Any prime Fibonacci number must have a subscript which is prime with one exception. (Go and find it out yourself. ;-) )
10) Can you find out Fibonacci numbers from Pascal's traingle?

There are lot more of such properties in The Art of Computer Programming by D. Knuth.
One of the interesting problem I found in the excercises of this book is
Problem) 2 players complete is a game: There a pile of n chips; 1st player takes as many chips as he like, except he can't take the whole pile.
From then on, players alternate moves, each person can take atmost twice as many chips as the preceeding player has taken. The player who takes the last chip wins.
Now solve this problem ;-)....do you see the usage of Fibonacci numbers here?
Some more properties. Basically you see such questions in interviews ;-)
1) The number of ways of picking a set (including the empty set) from the numbers 1, 2, ..., n without picking two consecutive numbers is F_(n+2). The number of ways of picking a set (including the empty set) from the numbers 1, 2, ..., n without picking two consecutive numbers (where 1 and n are now consecutive) is L_n==F_(n+1)+F_(n-1), where L_n is a Lucas number.
2) The probability of not getting two heads in a row in n tosses of a coin is F_(n+2)/2^n (Honsberger 1985, pp. 120-122). Fibonacci numbers are also related to the number of ways in which n coin tosses can be made such that there are not three consecutive heads or tails. The number of ideals of an n-element fence poset is the Fibonacci number F_n.
3) Given a resistor network of n 1-Omega resistors, each incrementally connected in series or parallel to the preceding resistors, then the net resistance is a rational number having maximum possible denominator of F_(n+1).
Do you know about Fibonacci number system? No I won't mention it here. Go find it yourself :-P
(Hint: search for Fibonaccimal)
Do you realize. KM to Mile conversion we can use Fibonacci numbers?
Yes. 8 Kms is 5 miles, 5 kms is 3 miles....So F(n) Kms is F(n-1) miles!!
What if you have to find 20 Kms in miles. Yep there a solution. convert to Fibonacci number system.
20 can be expressed as 13+5+2. So the miles conversion is 8+3+1=12Miles!!
Note: These are just approximations in Miles, not close values.
Now don't ask me what the value of 1Km in Miles ;-) ...larger values get closer but not accurate approximation.
visit this link for more info
Fibonacci numbers:
http://mathworld.wolfram.com/FibonacciNumber.html
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibrep.html
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/Fibonomials.html
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html
Phyllotaxis:
http://mathworld.wolfram.com/Phyllotaxis.html
http://maven.smith.edu/~phyllo/index.html
Fibonacci numbers in nature:
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
Fibonaccimal Base:
http://acm.up.pt/local/prova2/c.html
Books:
The Art of computer programming, Volume I, by D. Knuth.
Saturday, August 05, 2006
Kodanda Ramlayam in Tirupati.
Today I visited one of the oldest temples in the god's own city...Tirupati.
Yep I call this the god's own city. As there are lot of temples in and around this sacred town for hindus and each temple has lot of history.
The temple I visited is Kodanda Ramalayam.

This place has got some history. Once upon a time Jambavantha saw a cave in this place and observed some light glowing inside the cave. He asked Srirama about the light and Rama said its shows the presence of god. Later Jambavantha installed an idol of lord rama in the cave.
It was not noticed till SriKrishna devaraya's time. Srikrishna devaraya constructed a beautiful temple for lord Rama.
The following symbol (Raja mudrika: A pig and a knife is the rajamudrika for Srikrishna Devaraya) shows us the temple was infact constructed by SriKrishna Devaraya.

A wonderful place, clam and serene environment. I would suggest visitors to Tirupati to visit this temple as well. Opposite to this temple theres a Anjaneya swami temple. The road outside the temple leads to Alipiri...one straight road about 2 kms max. I guess this road is called SD Road.
Yep I call this the god's own city. As there are lot of temples in and around this sacred town for hindus and each temple has lot of history.
The temple I visited is Kodanda Ramalayam.

This place has got some history. Once upon a time Jambavantha saw a cave in this place and observed some light glowing inside the cave. He asked Srirama about the light and Rama said its shows the presence of god. Later Jambavantha installed an idol of lord rama in the cave.
It was not noticed till SriKrishna devaraya's time. Srikrishna devaraya constructed a beautiful temple for lord Rama.
The following symbol (Raja mudrika: A pig and a knife is the rajamudrika for Srikrishna Devaraya) shows us the temple was infact constructed by SriKrishna Devaraya.

A wonderful place, clam and serene environment. I would suggest visitors to Tirupati to visit this temple as well. Opposite to this temple theres a Anjaneya swami temple. The road outside the temple leads to Alipiri...one straight road about 2 kms max. I guess this road is called SD Road.
Subscribe to:
Comments (Atom)